โดเมน (Domain) และ เรนจ์ (พิสัย) (Range) https://coolaun.com/mathvacab/function/
วันอาทิตย์ที่ 23 กรกฎาคม พ.ศ. 2560
ความสัมพันธ์และฟังก์ชัน
ความสัมพันธ์ (Relation)r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A x B
โดเมน (Domain) และ เรนจ์ (พิสัย) (Range) https://coolaun.com/mathvacab/function/

โดเมน (Domain) และ เรนจ์ (พิสัย) (Range) https://coolaun.com/mathvacab/function/
การให้เหตุผล
การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำhttps://coolaun.com/m4/basic41/reason/

จำนวนจริง
มีหลักเกณฑ์ในการแบ่งจำนวนจริงอยู่หลายเกณฑ์ เช่น จำนวนตรรกยะ หรือ จำนวนอตรรกยะ; จำนวนพีชคณิต (algebraic number) หรือ จำนวนอดิศัย; และ จำนวนบวก จำนวนลบ หรือ ศูนย์
จำนวนจริงแทนปริมาณที่ต่อเนื่องกัน โดยทฤษฎีอาจแทนได้ด้วยทศนิยมไม่รู้จบ และมักจะเขียนในรูจำนวนจริง

จำนวนจริงแทนปริมาณที่ต่อเนื่องกัน โดยทฤษฎีอาจแทนได้ด้วยทศนิยมไม่รู้จบ และมักจะเขียนในรูจำนวนจริง
การให้เห็นผลแบบนิรนัย
การให้เหตุผลแบบนิรนัย (อังกฤษ: Deductive reasoning) หรือ การให้เหตุผลจากบนลงล่าง (อังกฤษ: top-down logic) เป็นการนำความรู้พื้นฐานซึ่งอาจเป็นกฎ ข้อตกลง ความเชื่อ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผการให้เห็นผลแบบนิรนัย

สมบัติการบวกและการคูณ
ถ้า a และ b เป็นจำนวนเต็มบวกใด ๆ แล้ว
a + b = b + a (สมบัติการสลับที่ของการบวก) เช่น 2 + 5 = 7 และ 5+ 2 = 7 ดังนั้น 2+5 = 5+2
a
 b = b
b = b  a (สมบัติการ
a (สมบัติการสมบัติการบวกและการคูณ
ฟังก์ชันเชิงเส้น
ในคณิตศาสตร์ขั้นสูง ฟังก์ชันเชิงเส้น หมายถึง ฟังก์ชันที่เป็น ฟังก์ชันเชิงเส้น มักหมายถึง คณิตศาสตร์ ที่เป็น กาเวกเตอร์ คือ ฟังก์ชันเชิงเส้นจะเป็นบรรดาฟังก์ชัน ที่แสดงได้ในรูปร่าง ฟังก์ชันเชิงเส้น
คือ ฟังก์ชันเชิงเส้นจะเป็นบรรดาฟังก์ชัน ที่แสดงได้ในรูปร่าง ฟังก์ชันเชิงเส้น
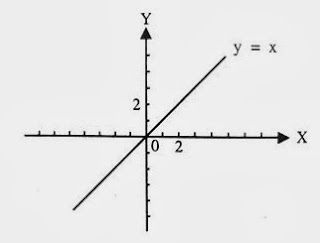
 คือ ฟังก์ชันเชิงเส้นจะเป็นบรรดาฟังก์ชัน ที่แสดงได้ในรูปร่าง ฟังก์ชันเชิงเส้น
คือ ฟังก์ชันเชิงเส้นจะเป็นบรรดาฟังก์ชัน ที่แสดงได้ในรูปร่าง ฟังก์ชันเชิงเส้น
สมัครสมาชิก:
ความคิดเห็น (Atom)
